Counterfeit Detection Using SpI
Range-Targeting Algorithms
by: Ryan Fattini | SpotFakeHandbags.com | 1/15/2012


For an authenticator, utilizing spi (stitches per inch) comparisons for detecting counterfeit merchandise can be a powerful tool. This is generally accomplished by comparing the spi of an authentic item to the spi count on an unknown item, and if the item in question does not share the same spi count as the authentic item, the item in question will then be red flagged. The problem with this method is that authentic items will not always share the same spi count, and therefore the "exact match" method can yield many false negatives. Therefore, to optimize this detection method, we will test two algorithms, both of which are designed to filter out counterfeit merchandise by targeting an acceptable spi range, rather than relying on exact match comparisons. The argument behind the SpI algorithm is as follows: (1) Larger spi values will increase the quality of the item, as well as increase the cost to the manufacturer. (2) Counterfeit merchandise is generally manufactured with cheaper materials, at lower costs, and is considered lower quality, (3) Therefore, we expect to find that the majority of counterfeit items will have lower spi values than authentic items.
Below we will support our first premise, by demonstrating that the higher the spi value, the stronger the seam and better the general quality, and as such, increased spi values become a greater manufacturing expense. Therefore, counterfeiters seeking the least expensive avenue for production may opt for lower spi values. By contrast, when targeting optimal quality, we should expect the high(est)-end designers opting for higher spi values.
Furthermore, in the fashion industry, it is understood that spi counts are not arbitrarily set, as their values are proportional to the strength of the seam. When a designer is notating the manufacturing specifications, the spi counts should be assigned in the item's blueprint. (Therefore, the heavily counterfeited, high-end designers such as Chanel or Louis Vuitton will have their item’s spi values in the manufacturing specifications), which is primarily based on seam strength (American & Efird, Inc. 2002).
Seam strength = SPI * (Thread Strength [lbs.] * F)
| SPI | 6 | 8 | 10 | 12 |
| Est. seam strength | 25.2 lbs. | 33.6 lbs. | 42 lbs. | 50.4 lbs. |
(ii) Lock stitch value (1.5) was used for table
(iii) Thread strength = 2.8
Premise 1): Higher spi values equal greater quality and greater cost for the manufacturer.
- “[Higher Spi values] will also consume more thread for every inch of sewn seam.” [1]
- “[Higher Spi values] used in a seam requires longer sewing cycles to complete the seam [...] Longer sewing cycles translate into higher labor costs and lower production levels.” [1]
- “[Higher SpI values] will contribute to higher seam strength and more elastic seams. Using the correct number of stitches per inch can greatly enhance the strength, appearance, and performance of the seam for a given fabric type and application.” [1]
We then should expect to see the high(est)-end designers using the more costly but higher quality larger spi values, and the counterfeiters using the faster and more cost efficient lower spi values. If an authenticator could obtain the spi values from manufacturer specifications, for a particular item, counterfeit detection would be easier. However, a designer releasing manufacturing data would be giving away the valuable blueprints of their products to everyone from competitor to counterfeiter. Therefore the purpose of the SpI filter will be to provide a universal gauge applicable to all designer merchandise that will output a probabilistic determination of authenticity based on competing spi values.
Such that to identify counterfeit signatures on the basis of spi values, we will need to develop a reasonable upper and lower bound spi threshold which will set the boundaries for the algorithm’s target zone. The threshold values will be drawn from universally recommended spi ranges based on the aforementioned seam strength formula.
Table (I): Recommended SPI values for various items: [1]
| Items | SPI | Stitch range pop. |
| Slacks, dresses, skirts | 3-5 | 2 |
| Buttonhole | 85-90 | 5 |
| Buttonsew | 16 | 0 |
| Blouses, tops | 10-14 | 4 |
| Childrenswear | 8-10 | 2 |
| Denim jackets, jeans etc. | 7-8 | 1 |
| Dress shirt, blouse | 14-20 | 6 |
| Dresses, skirts | 10-12 | 2 |
| Twill pants, shorts | 8-10 | 2 |
| Trousers, dress pants | 10-12 | 2 |
Table (I) provides a list of the recommended spi ranges for their respective garments, along with the population of the specific stitch ranges.
Based on the recommended (acceptable) spi ranges, we find that the majority of spi ranges will fall within ± 1-4 stitches. The mean representing 2.6 stitches.
Figure (II): (Gaussian) distribution of stitch range population.
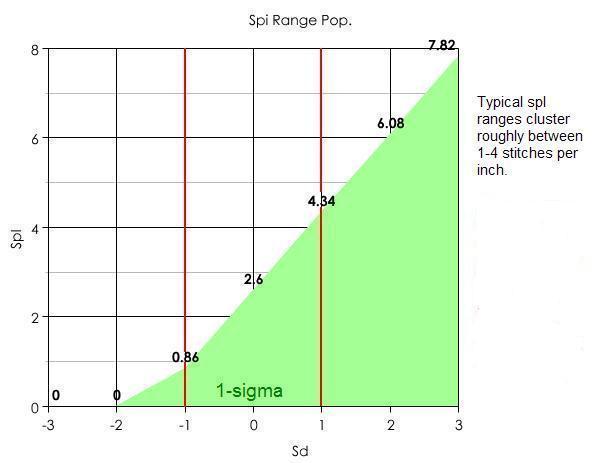
(i) However, setting the spi target zone to [authentic_spi ± 1-4 stitches] would swamp the SpI filter with false positives. Rather, to tighten up the filter and decrease the false positives, we will use the mean of the lower and upper bound stitch percentages (as percentages of each other) to locate a threshold.
(ii) Values derived from stitch range population [Table(I)]. Such that for an spi range of 8-10, (8/10 = .8 = (L)Lower Bound) and (10/8 = 1.25 = (h)Upper Bound).
Figure(III): Lower bound population:
Figure (IIII): Upper bound population:
Table (V): SPI thresholding
| Notation | Stitch range pop. | Lower bound stitch(L) | Upper bound stitch (h) |
| μ | 2.6 | .7099 | 1.157 |
| σ =1 | 1.74 | .2539 | .4186 |
| σ² | 3.04 | .0644 | .1752 |
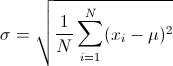
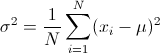
The lower bound mean (μ) clusters around 70% of the upper stitch count. And the upper bound mean (μ) at around 115% of the low bound stitch. Such that spI values on similar items do not have to match exactly stitch for stitch. This gives the designers a (tight) spi range to work within before quality (seam strength) is noticeably compromised. The goal of the SpI filter is to target this range and red flag any spi value that breaches the threshold. First we will make some assumptions about spi.
- For universal accuracy, the [Spi] filter will be dependant on the assumption that brand specific spi values will cluster in a fairly consistent manner with other similar brands. In many cases, we will be dealing with the high(est)-end designer merchandise traded in the global marketplace, i.e. Louis Vuitton, Chanel, etc, and we will assume that these brands will be relatively consistent on a spi quality scale with each other.
- Since we know that quality is a major component of the high(est)-end designer items in the global marketplace, we will assume that their merchandise's respective spi values preset in their manufacturing specifications will cluster closer to the acceptable upper bound stitch threshold than the acceptable lower bound threshold, of what would be considered an acceptable spi range based on the seam strength formula.
Therefore when comparing an unknown item to a similar authentic item, we will use an authentic spi value, (taken from a comparable, and verified authentic product, i.e. authentic Speedy 30 bag against unknown Speedy 30 bag), to anchor the range that the unknown item should target. We will try two filter methods, one more liberal (Thomas) and one more conservative (Margaret) .
The spi range in the liberal SpIT filter (Thomas) will then be set by:
A = spi of authentic item
X = spi of unknown item
X_Pass = spi of X hits target zone
The acceptable spi target zone boundaries were shifted slightly higher (within 1-sigma). This was done to eliminate direct spi hits on or around the lower bound, based on our assumption that the high(est)-end designers will cluster around the upper bounds of acceptable spi ranges. Therefore the SpI filter is more likely to eliminate false positives at a higher rate than false negatives. We will also use a more conservative method, one that tightens up the lower bound threshold further.
Conservative SpI filter formula (Margaret):
Lockstitch = 1.5
[Chain stitch = 1.7]
Trial run of both filters:
*[1 = outcome of filter true | 0 = outcome of filter false | + = false positive | - = false negative]
* Both spi values will pass through each filter.
| Item | Real (A) | Fake (X) | SPI | Marg filter | Tom filter | Pass | Fail | Filter accuracy |
| bal. test 1 | X | X | A39, X18 | X | - | - | X | 1 [3] |
| bal. test 2 | X | X | A39, X18 | - | X | - | X | 1 |
| bebe 1 | X | X | A12, X8 | X | - | - | X | 1 [4] |
| bebe 2 | X | X | A12, X8 | - | X | - | X | 1 |
| Val 1 | X, X | - | A18, A15 | X | - | - | X | 0- [2] |
| Val 2 | X, X | - | A18, A15 | - | X | X | - | 1 |
| Juicy 1 | X | X | A9, X7 | X | - | - | X | 1 [5] |
| Juicy 2 | X | X | A9, X7 | - | X | - | X | 1 |
| LV 1 | X, X | - | A4.8, A4 | X | - | - | X | 0- [6] |
| LV 2 | X, X | - | A4.8, A4 | - | X | X | - | 1 |
| Val 3 | X | X | A22, X26 | X | - | - | X | 1 |
| Val 4 | X | X | A22, X26 | - | X | - | X | 1 |
| Coach 1 | X | X | A20, X17 | X | - | - | X | 1 |
| Coach 2 | X | X | A20, X17 | - | X | X | - | 0+ [7] |
| Coach 3 | X, X | - | A20, A19 | X | - | X | - | 1 |
| Coach 4 | X, X | - | A20, A19 | - | X | X | - | 1 |
| Gucci 1 | X | X | A13, X10 | X | - | - | X | 1 [8] |
| Gucci 2 | X | X | A13, X10 | - | X | - | X | 1 |
| Fendi 1 | X | X | A10, X8 | X | - | - | X | 1 [9] |
| Fendi 2 | X | X | A10, X8 | - | X | - | X | 1 |
† Note that in some trial runs, authentic bags were compared to other authentic bags [A,A]. This is to demonstrate that authentic bags will not always have exact stitch matches. More spi comparison info here.
The results of the trial run were 17 true (1) readings and 3 false (0). Of the three false outputs, 2 were false negatives by Marg, and one was a false positive from Thomas. It appears to be the case that Tom performs most accurate with smaller spi values, and Marg with higher values.
So an initial threshold can be determined whereas lower spi values are fed to Tom, and higher spi values are fed to Marg. When we set the threshold to 15, such that when either spi value is ≤ 15, the set is fed to Tom, and if both spi values are > 15, the set is fed to Marg.
When we re-run the trial with this threshold, we get 20 true and 0 false.
Therefore the spi threshold T will be set to 15:
[t(SpI)] Filter: Here
Problems and issues:
- The SpI filter is not a precise calculation, it acts as a guideline, and therefore should not be used to ultimately decide the fate of an item.
- False positives and negatives are always possible. The better the fake, the more likely it will hit the authentic spi target.
- Slightly more freedom is given to an item that exceeds the upper bound threshold than the lower. The liberal upper bound threshold is directly tied to the seam strength formula, whereas we find that the higher the spi value, the higher the overall quality, (and subsequently the more money it will cost in materials), therefore it is more likely that a fake handbag will breach the lower bound threshold than the upper, as well as the likelihood that a high end designer may decide to incorporate more stitches and not less. However, on occasion some fakes will breach the upper bound threshold. [2][10]
- If an item does not pass, this does not = fake. If an item passes, this does not = authentic. The filter is an aid to the overall authentication process.
- Incorporate input based on the materials of the item.
Resources:
[1]: http://www.dewellton.com/images/Stitch_Guide/Stitch%20Length.pdf
[2]: http://spotfakehandbags.com/spot-fake-valentino-red-label.html
[3]: http://spotfakehandbags.com/fakebalenciaga-two.html
[4]: http://spotfakehandbags.com/spot-fake-bebe-retail-tag
[5]: http://spotfakehandbags.com/fakejuicy.html
[6]: http://spotfakehandbags.com/how-to-spot-fake-louis-vuitton-damier-handbags.html
[7]: http://spotfakehandbags.com/fakecoach-two.html
[8]: http://spotfakehandbags.com/fakegucci.html
[9]: http://spotfakehandbags.com/fakefendi.html
[10]:http://spotfakehandbags.com/spot-fake-louis-vuitton-belt-buckle
[11]:http://spotfakehandbags.com/how-to-spot-fake-coach-sneakers-shoes.html [12]:http://spotfakehandbags.com/spot-fake-hermes-label-logo.html
Copyright © spotfakehandbags.com 2012-2013, All rights reserved. PRIVACY POLICY | Site Nav